Speech science has a long history. Voice acoustics are an active area of research in many labs, including our own, which studies singing acoustics, as well as the speaking voice. This document gives an introduction and overview. This is followed by a more detailed account, sometimes using experimental data to illustrate the main points. Throughout, a number of simple experiments are suggested to the reader. As background, this link gives a brief multi-media introduction to the operation of the human voice.
Introduction and overview
It is common to think of the voice as involving two almost separate processes: one produces an initial sound and another modifies it. For example, at the larynx (sometimes called ‘voice box’), we produce a sound whose spectrum contains many different frequencies. Then, using tongue, teeth, lips, velum etc, (collectively called articulators) we modify the spectrum of that sound over time. In this simple introduction to the voice, we discuss the operations of first the ‘source’ of the sound, then of the ‘filter’ that modifies its spectrum, then of interactions between these. In a second part, we then return to look at the components in more detail.
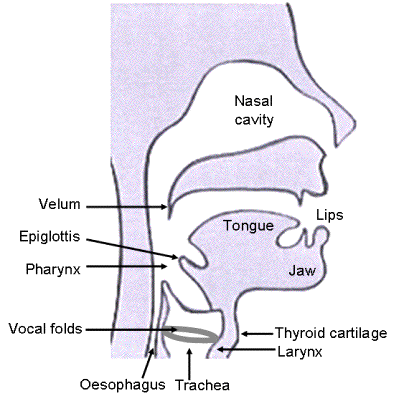
The source
There are several sources of sound in speaking. The energy usually comes from air expelled from the lungs. At the larynx, this flow passes between the vocal folds.
In voiced speech, the vocal folds (sometimes misleadingly called ‘vocal cords’) vibrate. This allows puffs of air to pass, which produces sound waves. Here is the first of a series of experiments (colour coded in the text): place your fingers on your neck near your larynx (on your ‘Adam’s apple’) then sing or speak loudly. Can you feel the vibration? The vibrations produced in voiced speech usually contain a set of different frequencies called harmonics. (See Sound spectrum.)
In whispering, the folds do not vibrate, but are held close together. This produces a turbulent (irregular) flow of air. This in turn makes a sound comprising a mixture of very many frequencies, which is called broad band sound. This gives the ‘windy’ sound that is characteristic of whispering. Try some experiments: can you whisper a note? What are the differences between speaking very softly and whispering loudly? Can you feel the vibration in your neck when you whisper? Can you sing in a whisper?
This allows us to divide speech sounds into voiced, meaning that the vocal folds vibrate, and unvoiced.
In pronouncing some sounds, such as the ‘f’ and ‘ss’ in the word ‘fuss’, turbulence is produced elsewhere: between teeth and lips in ‘f’ and between tongue and hard palate in ‘ss’. Both of these are unvoiced phonemes. (A phoneme is an element of speech sound; unvoiced means that the vocal folds don’t vibrate.) Next experiment: try sustaining these sounds while feeling for vocal fold vibration. The ‘p’ and ‘t’ in ‘pit’ are also unvoiced phonemes but here the source of sound is related to the sudden opening or closing of the air path.
Some voiced phonemes, such as vowel sounds in normal speech, use vibrations of the vocal folds with relatively little turbulence. In others, such as the ‘v’ and ‘z’ in ‘viz’ or the ‘b’ and ‘d’ in ‘bid’ combining both the sound from the larynx and the sound from the constriction. Another experiment: In whispered speech, by definition, no phonemes are voiced, so the differences between ‘pit’ and ‘bid’ disappear. Listen for the difference in normal and whispered speech. Then try some more examples using this table.

The table compares some pairs of phonemes that are pronounced with (nearly) the same articulation either with vocal fold vibration (voiced) or without vibration (unvoiced).
In fricatives, the tract is so constricted (by tongue, palate, teeth, lips or a combination) that sustained turbulent flow contributes broad-band sound to the spectrum. Plosives involve opening and/or closing of the tract with the lips (p, b) or the tongue (t, d; k, g) at different places of articulation. The sudden opening or closing and associated turbulence briefly produce broad band sound in plosives.
The filter
The sound of the ‘source’ interacts with the ‘filter’ (and also, as we’ll see later, vice versa). Depending on how you position your tongue and the shape of your mouth opening, different frequencies will be radiated out of the mouth more or less well. Another experiment: sing a sustained note at constant pitch and loudness, while varying the opening of your mouth and the position of the tongue. This will allow you to produce most of the vowels of English and some other phonemes, such as the ‘ll’ in ‘all’ or the ‘r’ in ‘or’, as pronounced in some accents.
How you position your velum (soft palate) also makes a difference. In the normal (high) position, all of the air and sound goes through the mouth. Lower it and you connect the nasal pathway to the mouth and lower vocal tract. Lower it further and you seal the mouth off from the pathway from nose to larynx. For the next experiment, observe the differences between a nasal sound (‘ng’) and a non-nasal one (‘ah’), then try sealing and unsealing your nose with your fingers, and also opening and closing your mouth, which will tell you how completely your velum seals one of the pathways.
Vowels
To a large extent, vowels in English are determined by how much the mouth is opened, and where the tongue constricts the passage through the mouth: front, back or in between. One can ‘map’ the vowels in terms of these articulatory details, or in terms of acoustic parameters that are closely related to them. Here are ‘maps’ for two different accents of English.
The frequencies on the axes correspond to bands of frequencies that are efficiently radiated, about which more later. The vertical axis on these graphs roughly corresponds to the jaw position (high or low) or the size of the lip opening. The horizontal axis corresponds to the position of the tongue constriction. We’ll return later to explain more about such maps, and how they may be obtained.
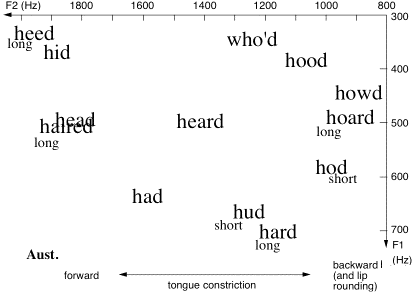
Vowel planes for two accents of English (Ghonim et al., 2007, 2013). These data were gathered in a large, automated survey in which respondents from the US (left) and Australia (right) identified synthesised words of the form h[vowel]d: a form in which most examples are real words. ‘short’ and ‘long’ indicate that more than 75% of the choices fell in these categories. You can map your own accent in this way on this web site.
Vowels and some other phonemes may be sustained over time: for them, the position of the articulators (and so the values of the well-radiated frequency bands) is relatively constant.
Consonants
For other phonemes (such as the ‘p, b, t, d’ discussed above), the change in articulation is important. Consequently, so are the variations with time of the associated frequency bands, as is the broad band sound associated with the opening or closing (Smits et al., 1996; Clark et al., 2007). In the examples ‘p, b, t, d’, the mouth opening is obviously changing during the consonant. Experiment: try slowing down (a lot) the motion of opening and closing and see if you notice what seems like a change in the vowel.
Like vowels, liquids (r and l) and nasal consonants (n, m, gn) are voiced and have a characteristic set of spectral peaks. For these, the tongue provides a narrower constriction.
In speech, vowels are in a sense less important than consonants: you can often understand a phrase even –f –ll v–w–l –nf–rm–t–n –s –bs–nt. On the other hand, vowels are more important in singing, because the vowel is sustained to produce a note.
Source-filter interactions
The separation of parts of the voice function into ‘source’ and ‘filter’ is practical, but one should remember that the distinction is incomplete. For instance, the geometry of the vocal folds affects not only the operation of the folds and thus the source, but also affects the acoustic properties of the ‘filter’. The geometry of the vocal and nasal tracts determines how they filter the sound, but the acoustical properties resulting from this geometry are thought to affect the operation of the vocal folds. We talk about these complications below.
Contrasting the voice with wind instruments
If we neglect the influence of the articulators on the larynx, we have the Source-Filter model. Superficially, it may seem obvious to a singer that the larynx and the articulators are independent: to many singers, particularly men in the low range, it seems that we can vary the pitch (~ the source) and vowel (~ the resonator/ filter) independently.
In contrast, an analogous argument would seem a very odd approximation to someone who plays brass instruments. A trombonist knows that the resonances in the bore of the instrument (~ the resonator/ filter) do indeed affect the motion of the player’s lips (~ the source). In fact, a brass player’s lips generally tend to oscillate at one of the frequencies of resonances in the bore. (See Acoustics of Brass Instruments) We shall return to this below, but let’s first note the following important quantitative difference between the two.
A trombone has a range that overlaps that of a man’s voice. However, the trombone is longer (a few metres) than a man’s vocal tract (0.2 m). The range of fundamental frequencies of the trombone lies within the range of the bore resonances. The range of the voice, especially of a man’s voice, usually lies below the frequencies of the vocal tract resonances. You are probably thinking that this difference – and therefore the approximation that the resonator doesn’t affect the source – is most questionable for high pitches, when the fundamental of the voice enters the range of vocal tract resonances. You’re right, and we’ll come back to this.
The Source-Filter model
In the (simplest version of the) Source-Filter model (Fant 1960), interactions between sound waves in the mouth and the source of sound are neglected. Although oversimplified, this model explains many important characteristics of voice production.
The figure below is an experimental illustration of the Source Filter model, using 3D-printed models of two configurations of a vocal tract, corresponding to the vowels in the words ‘had’ and ‘heard’. (Click on diagram for a higher resolution version.) The source – the periodic laryngeal flow – was synthesised, then measured as it was input to the model tracts. Because the laryngeal flow is periodic, its spectrum is made up of harmonics. The output at the ‘lips’ was also measured. The gain functions (the transpedance) of the tracts were measured independently. They are shown below in both the time and frequency domains.
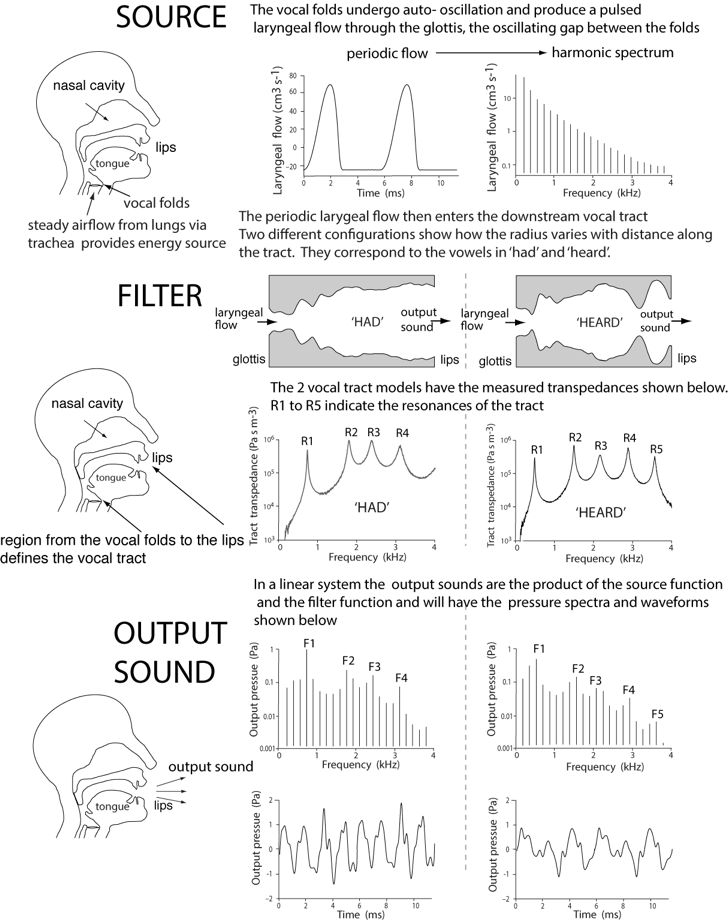
Experimental illustration of the simple Source-FIlter model. The graphs in this figure were all measured experimentally. Details are in the paper “An experimentally measured Source-Filter model: glottal flow, vocal tract gain and radiated sound from a physical model,” Wolfe, J., Chu, D., Chen, J.-M. and Smith J. (2016) Acoust. Australia, 44, 187–191. It is available for reprint, with acknowledgment.
Notice how the formants in the output sound (F1 to F4 or F5) correspond approximately to the peaks in the gain function due to resonances (R1 to R4 or R5). Notice too that the output sound is periodic, but that it is difficult to identify other features in the time domain.
As noted, the measurements above use 3D printed models of the tracts (and indeed, books and papers on phonetics usually just show cartoon sketches). Is it possible to use direct measurements on real vocal tracts? The answer is that we can’t do it directly. However, we can make indirect measurements. We can’t measure the flow spectrum through the larynx, but we can measure the vibration of the vocal folds. Here, we do that using an electroglottograph (EGG): we apply a small radio frequency voltage across the neck using skin electrodes at the level of the vocal folds. The magnitude of the current that flows varies as the folds come into contact and separate. The spectra and sound files at the top of the figure are an EGG signal. Below that, we show the results of measurements of the resonances of the vocal tract, made at the mouth, during speech. This gives a quasi-continuous line whose peaks identify the resonances. It also shows the harmonics of the voice. Below that are the spectra measured for that particular vowel, in the same gesture.
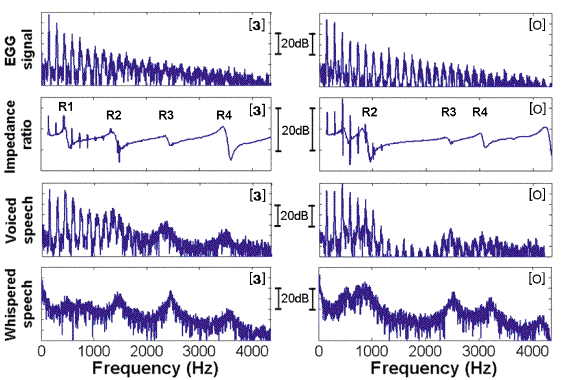
ere we contrast two vowels: At left is the vowel [3], as in ‘heard’ (like one example used in the preceding figure). At right, [o], as in ‘hot’. The top graphs and sound files are for experimental measurements of the vocal fold contact. Note that this measurement of the source shows little difference between the two vowels: the filter has little or no effect on the source. The next pair of graphs are measurements of the vocal tract, made from the mouth, during the vowel. (More on this technique here.) The broad peaks identify resonances of the vocal tract, the sharp lines are the harmonics. Here, because the tract is in a different configuration for the two vowels, the resonances occur at different frequencies. The next two rows show the voice output for voiced speech and for whispering, measured in the same vocal gesture. More detail on these examples here.
So, to summarise, the spectrum of the output sound depends on the spectrum of the laryngeal source, on the frequency dependent ‘gain’ of the vocal tract, including the efficiency of radiation from the mouth and nose. Although we have not yet mentioned it, it also depends on interactions among these. We shall discuss these in the more detailed sections below.
Some difficulties
Before we leave this brief overview, it is worth noting that there is still much about the voice that is still incompletely understood. One of the reasons for this is the difficulties of doing experiments. Some of the data that we should like to know – the gain function of the vocal tract sketched above, the mass and force distribution in the vocal folds, for instance – are impossible to measure while the voice is operating, not only ethically but practically.
For most human physiology, much information has been obtained from other species, whose organs function in similar ways. When it comes to the voice, however, there is no such similar species – no-one is very interested in the voice of the lab rat. Much of our knowledge comes from experiments using just the sound of the voice as experimental input. Other knowledge comes from medical imaging. Another approach is to use a mathematical model: one can treat the vocal folds as collections of masses on springs, and the vocal tract as an oddly shaped pipe that transmits sound. The next step is to solve the equations for this simple system and to predict the sound it would make, and to see how this correlates with sounds of speech or singing. Another is to make artificial systems with the shape of the vocal tract and some sort of aero-mechanical oscillator at the position of the glottis. Yet other knowledge comes from other experiments and observations that are often, for practical and ethical reasons, somewhat indirect. Because of the importance of the human voice, these are all active research areas.
We now look more closely at some of the topics introduced above. Other reviews are given by, for example, Lieberman and Blumenstein, 1988; Stevens, 1999; Hardcastle and Laver, 1999; Johnson, 2003; Clark et al., 2007; Wolfe el al, 2009.
The source at the larynx
To speak or to sing, we usually expel air from the lungs. The air passes between the vocal folds, which are muscular tissues in the larynx. If we get the air pressure and the tension and position of the vocal folds just right, the folds vibrate at acoustic frequencies. This means we have an oscillating valve, letting puffs of air flow into the vocal tract at some frequency fo.
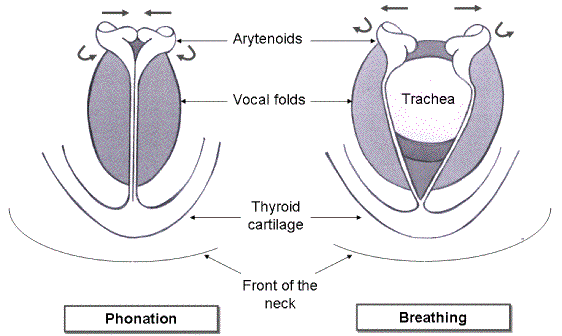
Technically, we move the arytenoid cartillages closer than their separated breathing position, which brings the vocal folds closer to each other, called adduction (Scherer 1991). This reduced aperture between the folds is called the glottis. Compared to the breathing position, the narrow glottis restricts the flow of air, which in turn means that the steady pressure drop across the larynx is greater when the aperture is small. The higher pressure drop means that the speed of air through the glottis is high, but the small cross section means that the volume flow (in litres per second) is less. Experiment: take a deep breath and time how quickly you can breathe it out completely with your larynx relaxed. Now do the same, while pronouncing a whispered ‘ah’ and singing a (loud) ‘ah’. Which breath lasts longest (i.e. which has the lowest flow)?
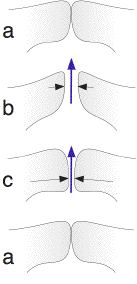
The schematic at right sketches the vocal folds in cross section. In (a), the pressure acting below the vocal folds tends to force them upwards and apart. Ths pressure difference is also responsible for accelerating air through the glottis to produce the high-speed air flow: the blue arrow in (b).
The rapid air flow through the glottis creates a suction (black arrows). This suction tends to draw the folds back together (via the ‘Bernoulli effect’, Van den Berg 1957), as does the tension in the folds themselves. These alternating effects tend to excite a cycle of closing and opening of the folds, which is assisted by the inherent springiness or elasticity of the folds (which provide a restoring force), their mass (which provides inertia) and the inertia of the air flow itself, which maintains high flow rates even as the folds are closing.
Depending on the acoustic impedance of the tracts above and below the folds, and on passive mechanical and geometric properties of the tissue, this can lead to self-sustained oscillation (Flanagan and Landgraf, 1968; Fletcher, 1979; Elliot and Bowsher, 1982; Boutin, Smith and Wolfe, 2015).
| Muscles do not directly vibrate the vocal folds, which is a passive effect described above (Van den Berg, 1958). However, muscles contribute to its control, by determining how much the folds are pushed together and how much they are stretched. If you get these parameters right, and hold them steady, you can produce a note with a fixed pitch, which means that the folds are vibrating in a regular, periodic way. That’s what we (usually) do in singing. In normal speech, the pitch varies during each syllable, usually in a smooth way.The fundamental frequency for speech ( fo) is typically 100 to 400 Hz. For singing, the range may be from about 60 Hz to over 1500 Hz, depending on the type of voice. The speed of sound c is about 340 m.s−1, so the wavelengths of the fundamentals (λ = c/f) are typically 1 to 3 metres, but can be as short as 0.3 m or less for high-pitched singing. So here is an important point: the wavelength is usually, but not always, much longer than the vocal tract itself, which is typically 0.15-0.20 m from mouth to glottis. This makes the voice very different from typical musical instruments: a man whose vocal tract is the size of piccolo still manages to produce a vocal range corresponding to that of a trombone or bassoon. In the artificial instruments, a vocal tract resonance largely controls the pitch. For the voice, the pressure provided by the lungs and the tension in the vocal folds together largely determine both loudness and pitch, but resonances in the vocal tract can make a big difference too, as we’ll see below. |
Different registers and vocal mechanisms
How to cover a wide range of pitch? Let’s compare with musical instruments. On a violin or guitar, one can change the length of a string, but to cover a large range, one can also cross to a new string. In trumpet, trombones, clarinets, flutes etc, one can change the length of a pipe (with valves, a slide or keys) but one can also change registers, which means changing the mode of vibration in the pipe.
In the voice, we can change the muscle tension and the pressure to vary the pitch. However, to cover a range of a few octaves, we usually need to use different registers (Garcia, 1855). The distinctions among registers in singing are not always clear, however, because changing registers corresponds to both laryngeal and vocal tract adjustments (Miller, 2000). The vocal folds can vibrate in (at least) four different ways, called mechanisms (Roubeau et al., 2004; Henrich, 2006).
- Mechanism 0 (M0) is also called ‘creak’ or ‘vocal fry’. Here the tension of the folds is so low that the vibration is not periodic (meaning that successive vibrations have substantially different lengths). M0 sounds low but has no clear pitch (Hollien and Michel, 1968). Experiment: if you hum softly the lowest note you can and then go lower, you will probably produce M0.
- Mechanism 1 (M1) is usually associated with what women singers call the ‘chest’ register and men call their normal voice. This is used to produce low and medium pitches. In M1, virtually all of the mass and length of the vocal folds vibrates (Behnke, 1880) and frequency is regulated by muscular tension (Hirano et al., 1970) but is also affected by air pressure. The glottis opens for a relatively short fraction of a vibration period (Henrich et al., 2005).
- Mechanism 2 (M2) is associated with the ‘head’ register of women and the‘falsetto’ register in men. It is used to produce medium and high pitches for women, and high frequencies for men. In M2, a reduced fraction of the vocal fold mass vibrates. The moving section involves about two thirds of their length, but less of the breadth. The glottis is open for a longer fraction of the vibration period (Henrich et al., 2005).
- Mechanism 3 (M3) is sometimes used to describe the production ofthe highest range of pitches, known as the ‘whistle’ or ‘flageolet’ register (not to be confused with whistling) (Miller and Shutte, 1993). Little has been published on this: we have been researching it lately and have published two papers on it (Garnier et al, 2010; 2012).
Although some people use M0 in speech, especially at the end of sentences, and coloratura sopranos use M3 in their highest range, speech and singing usually use M1 and M2. Men and women typically change from M1 to M2 at about 350-370 Hz (F4-F#4) (Sundberg, 1987), which is often called a ‘break’ in the voice. Consequently, with their lower overall range, men typically use M1 for nearly all speech and most singing. However, in some styles of pop music and some operatic styles, men use M2 extensively: men who sing alto are usually using M2. For women singers, the situation depends on vocal range. Sopranos sing in M2 and usually extend its range downwards to avoid the ‘break’ over their working range. High sopranos may use M3. Altos often use both M1 and M2.
There is usually a pitch and intensity range over which singers can use either M1 or M2 (Roubeau et al., 2004), and trained singers are good at disguising the transition. Sometimes, as in yodeling, the transition is a feature. Experiment: if you try to produce a smooth pitch change or glissando over your whole range, you will probably notice a discontinuity: a jump in pitch and a change in timbre at a pitch somewhere near the bottom of the treble clef. This is where you change from M1 to M2. At the pitch of that break, you may also produce a break by singing a crescendo or decrescendo at constant pitch (see Svec et al., 1999; Henrich, 2006).
Sopranos often have a considerable overlap region for M2 and M3. Those that sing with M3 also use a different form of resonance tuning in the high range. This gives a complicated set of possible strategies for singing in the high range (Garnier et al, 2010; 2012).
The next figure shows a spectrogram of a glissando through the four mechanisms.
A spectrogram plots frequency (vertical) against time (horizontal) with sound level in colour or grey-scale. This one shows the four laryngeal mechanisms on an ascending glissando sung by a soprano. Notice the discontinuities in frequency (clearer in the higher harmonics) at the boundaries M1-M2 and M2-M3. The horizontal axis is time, dark represents high power, and the horizontal bands in the broad band M0 section clearly show four broad peaks in the spectral envelope. These may also be seen to varying degrees in the subsequent harmonic sections. This glissando in wav. Spectrogram above in .jpg.
Producing a sound
The processes that convert the ‘DC’ or steady pressure in the lungs into ‘AC’ or oscillatory air flow and vocal fold vibration are necessarily nonlinear. First, the ‘Bernoulli’ suction between the folds is proportional to the square of the flow velocity (see this link). Second, the collision of the folds when the glottis closes is also highly nonlinear (Van den Berg, 1957; Flanagan and Landgraf, 1968; Elliot and Bowsher, 1982; Fletcher, 1993).
In science, linear just means that the equation is a straight line, so a change in one variable produces a proportional change in the other. We show elsewhere that an oscillator with a linear force law vibrate as in a pure sine wave, which has just one spectral component. Conversely, anything with a nonlinear force law does not vibrate sinusoidally, and so has more than one frequency component. For some non-scientists, linear and nonlinear have been confused by postmodernism, where the words are used metaphorically.
Because of these nonlinearitities, the fold vibration is nonsinusoidal and therefore has many frequency components. In M1, M2 and M3, the motion is (almost exactly) periodic, so the spectral components are harmonic: a microphone or flow meter placed at any point in the tract would indicate components at the fundamental frequency f0 and its harmonics 2f0, 3f0 etc, as shown in the figures above. (Follow this link for harmonic spectra.)
Generally, the amplitude of harmonics decreases with increasing frequency, though there are important exceptions. The negative slope in the spectral envelope (called the ‘spectral tilt’) is different for types of speech or singing (Klatt and Klatt, 1990). To some extent, this slope is compensated by the response of the human ear, which is usually more sensitive to the higher harmonics than to the fundamental (see Hearing). More power in the high harmonics makes a sound bright and clear; weakening the high harmonics makes a mellow, darker or muffled sound. If you have a sound system with bass and treble or tone controls, or a sound editing program, you can experiment with strengthening and weakening the high harmonics using the treble or tone control. (Some filtered voice sound examples here.)
A breathy voice has a spectrum with a strongly negative slope. This voice is produced when the glottis doesn’t close completely. The spectral envelope is flatter (the higher harmonics are less weak) in loud speech or singing, which have an abrupt closure of the vocal folds and a short open phase of the glottis (Childers and Lee, 1991; Gauffin and Sundberg, 1989, Novak and Vokral, 1995). This flatter spectrum has relatively more power in the frequency range 1–4 kHz, to which the ear is most sensitive.
It is possible to make high-speed video images of the vocal folds using an optical device (endoscope) inserted in either the mouth or nose (Baken and Orlikoff, 2000; Svec and Schutte, 1996). Electroglottography (Childers and Krishnamurthy, 1985), which is described above, is less invasive but less direct. Although the flow through the glottis cannot be measured, it can be estimated from the flow from the mouth and nose, which can be measured using a face mask (Rothenberg, 1973) or from the sound radiated from the mouth. Both techniques require inverse filtering (Miller 1959), which in turn requires knowledge of or assumptions about the acoustic effects of the vocal tract.
When is the source independent of the filter?
As explained above, one cannot do the direct experiments that would allow us to answer this question directly, so we are obliged to rely on indirect evidence, or on theoretical or numerical models.
In a simple model, Fletcher (1993) uses the ‘Bernoulli’ nonlinearity in a simple but general analysis of resonator-valve interaction with different valve geometries. He derives equations and inequalities relating the natural frequencies of the valve, the resonance frequency of the filter (or resonator) and the fundamental frequency of the sound produced. Treating the vocal folds (or a trombonist’s lips) as a valve that opens when the upstream pressure excess is increased, this model gives results consistent with what we know about the voice and trombones: when the resonance falls at a frequency slightly above that of the valve, a sufficiently strong resonance can ‘control’ the oscillation regime. If the resonances are at much higher frequencies, they have little influence on the fundamental frequency at which the valve vibrates.
Resonances, spectral peaks, formants, phonemes and timbre
Acoustic resonances in the vocal tract can produce peaks in the spectral envelope of the output sound. In speech science, the word ‘formant’ is used to describe either the spectral peak or the resonance that gives rise to it. In acoustics, it usually means the peak in the spectral envelope, which is the meaning on this site. We discuss the different uses in more detail on What is a formant?, but for the moment note that ‘formant’ should be used with care.
Phoneme
In non-tonal languages such as English, vowels are perceived largely according to the values of the formants F1 and F2 in the sound (Peterson and Barney; 1952, Nearey, 1989; Carlson et al., 1970). F3 has a smaller role in vowel identification. F4 and F5 affect the timbre of the voice, but have little influence on which vowel is heard ((Sundberg, 1970). We repeat below the plots of (F2,F1) for two accents of English. Note that, in these graphs, the axes do not point in the traditional Cartesian direction: instead, the origin is beyond the top right corner. The reason is historical: phoneticians have long plotted jaw height on the y axis and ‘fronting’, the place of tongue constriction, on the x. This choice maintains that tradition approximately.
These maps were obtained in a web experiment, in which listeners judge what vowel has been produced in synthetic words (Ghonim et al., 2007, 2013) in which F1, F2 and F3 are varied, as well as the vowel length and the pitch of the voice. Experiment: using that web site you can make a map of the vowel plane of your own accent.
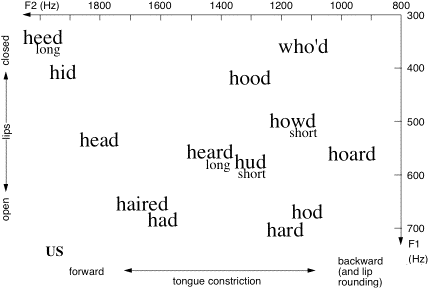
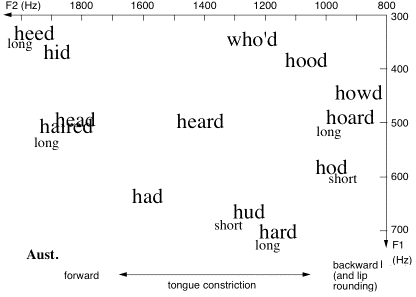
We repeat the figure showing the vowel planes for US and Australian English measured in an on-line survey (Ghonim et al., 2007).
The vocal tract as a pipe or duct
To understand how the resonances work in the voice, we can picture the vocal tract (from the glottis to the mouth) as a tube or acoustical waveguide. It has approximately constant length, typically 0.15-0.20 m long, a bit shorter for women and children. However, the cross section along the length varies in ways that can be varied by the geometry of the tongue, mouth etc. The frequencies of the resonances depend upon the shape. The frequencies of the first, second and ith resonances are called R1, R2, ..Ri.., and those of the spectral peaks produced by these resonances are called F1, F2, ..Fi… (See this link for a discussion of the terminology.)
When pronouncing vowels, R1 takes values typically between 200 Hz (small mouth opening) to 800 Hz. Increasing the mouth opening gives a large proportional increase in R1. Opening the mouth also affects R2, but this resonance is more strongly affected by the place at which the tongue most constricts the tract. Typical values of R2 for speech are from about 800 to 2000 Hz. The resonant frequencies can also be changed by rounding and spreading the lips or by raising or lowering the larynx (Sundberg, 1970; Fant, 1960).
We’ll return to discuss this below, but for the moment, let’s note that, if the open end of a tube is widened, the resonant frequencies rise, which explains the mouth effect. Similarly, reducing or enlarging the cross section near a pressure node respectively lowers or raises the resonance frequency. Conversely, reducing or enlarging the cross section near a pressure anti-node respectively raises or lowers the resonance frequency. This explains some features of the tongue constriction. The nasal tract has its own resonances, and the nasal (nose) and buccal (mouth) tracts together have different resonances. The lowering the velum or soft palate couples the two, which affects the spectral envelope of the output sound (Feng and Castelli, 1996; Chen, 1997).
Nasal vowels or consonants are produced by lowering the velum (or soft palate, see Figure 1). The nasal tract also exhibits resonances. Coupling the nasal to the oral cavity not only modifies the frequency and amplitude of the oral resonances, but also adds further resonances. The interaction can produce minima or pole-zeros of the vocal tract transfer function, with resultant minima or ‘holes’ in the spectrum of the output sound (Feng and Castelli, 1996; Chen, 1997).
Resonances, frequency, pitch and hearing
Some comments about frequency and hearing are appropriate here. The voice pitch we perceive depends largely on the spacing between adjacent harmonics, especially those harmonics with frequencies of several hundred Hz (Goldstein, 1973). For a periodic phonation, the harmonic spacing equals the fundamental frequency of the fold vibration, but the fundamental itself is not needed for pitch recognition.
Except for high voices, the fundamental usually falls below any of the resonances, and so may be weaker than one of the other harmonics. However, its presence is not needed to convey either phonemic information or prosody in speech. The pass band of telephones is typically about 300 to 4000 Hz, so the fundamental is usually absent or much attenuated. The loss of information carried by frequencies above 4000 Hz (e.g. the confusion of ‘f’ and ‘s’ when spelling a name) is noticed in telephone conversation, but the loss of low frequencies is much less important. (An experiment: next time you are put ‘on hold’ on the telephone, listen to the bass instruments in the music. Their fundamental frequencies are not carried by the telephone line. Can you hear their pitch? Of course, they are less ‘bassy’ than if you heard them live, but is the pitch any different?)
Our hearing is most sensitive for frequencies from 1000 to 4000 Hz. Consequently, the fundamentals of low voices, especially low men’s voices, contribute little to their loudness, which depends more on the power carried by harmonics that fall near resonances and especially those that fall in the range of high aural sensitivity. (Another experiment: you can test your own hearing sensitivity on this site.)
Timbre and singing
Varying the spectral envelope of the voice is part of the training for many singers. They may wish to enhance the energy in some frequency ranges, either to produce a desired sound, to produce a high sound level without a high energy input, or to produce different qualities of voice for different effects. Characteristic spectral peaks or tract resonances have been studied in different singing styles and techniques (Stone et al., 2003; Sundberg et al., 1993; Bloothooft and Pomp, 1986a; Hertegard et al., 1990; Steinhauer et al., 1992; Ekholm et al., 1998; Titze, 2001; Vurma and Ross, 2002; Titze et al., 2003; Bjorkner, 2006; Garnier et al., 2007b; Henrich et al., 2007). In this laboratory, we have been especially interested in three techniques: resonance tuning, harmonic singing and the singers formant.
The origin of vocal tract resonances
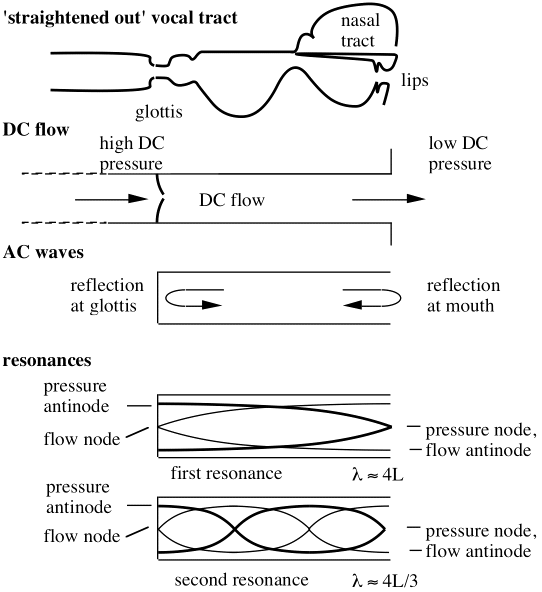
Vocal tract resonances (Ri) give rise to peaks in the output spectrum (Fi). However, the relation between Ri and Fi is a little subtle. For that reason, let’s consider the behaviour of some geometrically simple systems, for which acoustical properties can be more easily calculated, illustrated in the cartoons here and below. (This section follows Wolfe et al, 2009.)
In the top sketch, we have ‘straightened out’ the vocal tract. Below, it is modelled as a simple cylindrical pipe to explain, only qualitatively, the origin of the first two resonances. Below we give theoretical calculations for the input impedance spectrum and a transfer function for simplistic models of the vocal tract with length = 170 mm and radius = 15 mm. The dashed line is for a cylinder. When a circular ‘glottal’ constriction is added, with a radius of 2 mm and an effective length of 3 mm (including end effects), the result is the solid line. This figure is taken from Wolfe et al (2009).
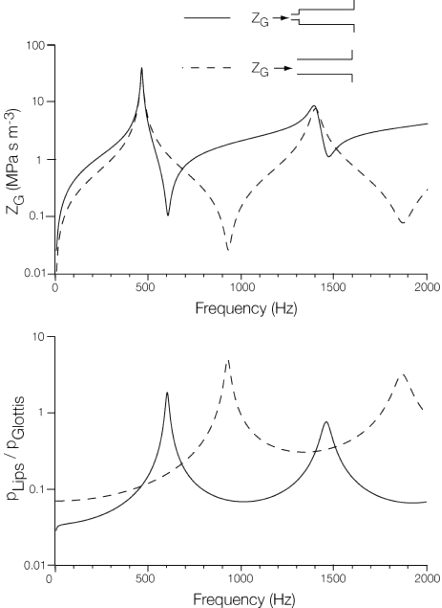
At this stage, it is helpful to introduce the acoustic impedance, Z, which is the ratio of sound pressure p to the oscillating component of the flow, U. (This link gives an introduction to acoustic impedance.) Z is large if a large variation in pressure is required to move air, and conversely. Z is a complex quantity, meaning that p and U are not necessarily in phase, so that Z has both a magnitude (shown in the plots at right) and a phase. The in-phase component (the real component when complex notation is used) represents conversion of sound energy into heat. Components that are 90° out of phase (imaginary components in complex notation) represent storage of energy. A small mass of air in a sound wave can store kinetic energy but, because of its inertia, pressure is required to accelerate it. It has an inertive impedance (p is 90° ahead of U, positive imaginary component). Flow of air into a small confined space increases the pressure, storing potential energy. This is compliant impedance (p is 90° behind U, negative imaginary component). When the dimensions of a duct are not negligible in comparison with the wavelength, p and U vary along its length. Z often varies strongly with frequency and the phase changes sign at each resonance.
Tract-wave interactions
Now the mouth is open to the outside world, but the sound wave is not completely ‘free’ to escape, because of Zrad, the impedance of the radiation field outside the mouth. A pressure p at the lips is required to accelerate a small mass of air just outside the mouth, so the inertance is not zero, but is usually Zrad small. At high frequency, however, larger accelerations are required for any given amplitude, so Zradincreases with frequency. In a confined space (inside the vocal tract), acoustic flow does not spread out, so impedances are usually rather higher than Zrad.
As we explain in this link, Z in a pipe (or in the vocal tract) depends strongly on reflections that occur at open or closed ends. A strong reflection occurs at the lips, going from generally high Z inside to low Zin the radiation field. Suppose that a pulse of high-pressure air is emitted from the glottis just when a high pressure burst pulse returns from a previous reflection: the pressures add and Z is high. Conversely, if a reflected pulse of suction cancels the input pressure excess, Z is small. This effect produces the large range of Z shown in the previous figure. High output levels occur at the lips when the input impedance Zis a minimum.
For the sake of simplicity, let’s imagine the tract as a tube, nearly closed at the glottis but open at the mouth. In fact, for /3/ (the vowel in the word “heard”), the resonances shown in the figure above fall at the frequencies expected for an open cylindrical tube of length 170 mm, open at the mouth and nearly closed at the glottis. Now, for a simple tube with length L, open at the far end, the behaviour is shown by the dashed line in the preceding figure. The wavelengths that give maxima in Z are approximately λ1 = 4L, λ3 = 4L/3, λ5 = 4L/5, etc and so at frequencies, f1 = c/4L, f3 = 3c/4L = 3f1, f5 = 5c/4L = 5f1, etc. Minima occur half way between the maxima.
Now let’s add the glottis, giving a local constriction at the input. The solid line shows the new input impedance Z. The maxima in Z (pressure antinodes or flow nodes) are hardly changed. This makes sense: a local constriction (of small volume) at the input has little effect on a maximum in Z, where flow is small. For modes where the flow is large, however, the air in the glottis must be accelerated by pressures acting on only a small area. So the frequencies of the minima in Z (pressure node, flow antinode) fall at lower frequencies. If the glottis is sufficiently small, Z(f) falls abruptly from each maximum to the next minimum, which thus occur at similar frequencies. So do the maxima in the transfer functions.
So far, we haven’t mentioned the impedance of the subglottal tract leading to the lungs. This is difficult to measure. However, there are good reasons to expect no strong resonances in the audio frequency range. The lungs have complicated geometry, with successively branching tubes, extending to quite small scale at the alveoli. This is expected to produce little reflection in the range of frequencies that interest us (see Fletcher et al., 2006). As mentioned above, many of the obvious experiments for studying vocal tract resonances are impossible. A number of less obvious techniques exist, however. One of our papers reviews these (Wolfe et al, 2009).
Tract-wave interactions: Do the ‘source’ and the ‘filter’ affect each other?
As we explained above, the resonances of the vocal tract occur at frequencies well above those of the fundamental frequency – at least for normal speech and low singing. Further, the frequencies of vocal fold vibration (which gives the voice its pitch) and those of the tract resonances (which determine the timbre and, as we have seen, the phonemes) are controlled in ways that are often nearly independent. In most singing styles, the words and melody of a song are prescribed. Conversely, in speech, we have the subjective impression that we can vary the prosody independently of the phoneme – for example, one can often replace a key word in a sentence without changing the prosody at all.
As mentioned above, the voice is unlike a trombone or other wind instrument*, in which one of the resonances of the air column drives the player’s lips or reed (respectively) at a frequency close to its resonant frequency. In the voice, there is usually no simple relation between the frequencies: a singer may cover a range of two or more octaves (i.e. vary the frequency by a factor of 4 or more) with relatively little change in the shape and size of the vocal tract. Further, although there is typically a difference of an octave (a factor of two in wavelength) between the fundamental frequencies of male and female singing voices, there is much smaller difference in the lengths of the tracts.
From this we can conclude that the resonances of the tract do not normally control the pitch frequency of the voice. Nevertheless, the glottal source and the vocal tract resonances may be interrelated in a number of ways. First, there are direct, physical interactions: the mode of phonation affects the reflections of sound waves at the glottis, and so affects standing waves in the tract (cf. Fig. 4). Second, pressure waves in the tract can influence the air flow through the glottis or the motion of the vocal folds. Third, there is the possibility that speakers and singers may consciously or unconsciously use combinations of fundamental frequency and resonance frequency for different effects, in particular to improve their efficiency. We discuss these in turn.
* Is there an acoustic instrument like the voice? Not really, but one can mention some similarities with the harmonica or mouth organ. In that instrument, the pitch is largely determined by mechanical properties of a metal reed that controls the air flow. The pitch may, however be affected by effects in the acoustic field nearby, e.g. cupping the hands over the instrument to ‘bend’ tones. Like the voice, the harmonica may produce sounds whose wavelengths are much larger than the size of the instrument and, like the voice, one can modify the spectral envelope by changing the geometry of the air space through which it radiates.

Does the glottis affect the tract resonances?
The glottis is very much smaller that the cross-section of the vocal tract, which is why, in the simplistic figure above, we treated the vocal tract as a pipe open at mouth and closed at glottis. This is an exaggeration, of course! The average opening of the glottis depends on what fraction of the time it is open (its ‘open quotient’) and how far it opens (Klatt and Klatt, 1990; Alku and Vilkman, 1996; Gauffin and Sundberg, 1989), which in turn depend on the voice register and pitch.
For a duct that is almost closed at one end and open at the other, the frequency of the first resonance increases as the opening increases. Various researchers have shown that, when the glottis is somewhat open for whispering, the resonance or formant peaks occur at higher frequencies (Kallail and Emanuel, 1984a,b; Matsuda and Kasuya, 1999; Itoh et al., 2002; Barney et al, 2007; Swerdlin et al., 2010).
Do pressure waves affect the vocal fold vibration?
This is an area in which it’s hard to do the experiments that would most clearly answer the question. However, there has been a lot of work on numerical models. Some of these predict that air through the glottis and the vocal fold vibrations depend on the pressure difference across the glottis and folds, and thus waves in the tract (Rothenberg, 1981; Titze, 1988, 2004). Not surprisingly, the phase of the pressure wave is important in these models: whether a pressure decrease outside the vocal folds will tend to open them will depend on when during a cycle it arrives.
Can one observe the effect of pressure waves on the motion of vocal folds experimentally? Hertegard et al., (2003) used an endoscope (camera looking down the throat) to film the larynx while singers mimed singing, and a tube sealed at the lips provided artificial pressure waves. They reported bigger vibrations when the pressure waves had frequencies near those of normal singing. In our lab (Wolfe and Smith, 2008), we used electroglottography (EGG, described above) to monitor the vocal fold vibration, and used a didjeridu to produce the pressure waves. We found that the didjeridu signal could drive the folds at a level comparable with those generated by singing. All the above evidence suggests that the standing waves in the ‘filter’ have a strong interaction with the source.
Do singers and speakers use tract resonances and pitch in a coordinated way?
If you want to sing or to speak loudly, you might want to take advantage of the resonances of the vocal tract to improve the efficiency with which energy is transmitted from the glottis to the outside sound field. The most studied example is the problem faced by sopranos. The range of R1 (about 300 to 800 Hz, roughly D4 to G5) overlaps approximately the range the soprano voice. If a soprano did nothing about this, she’d have a serious problem: First, for many note-vowel combinations, the f0 of the note would fall above R1. So she would lose the power boost from R1. This is particularly a difficulty for opera singers, who must compete with an orchestra, without the aid of a microphone. There is also the problem that her voice quality would tend to change when she crossed the R1 = f0 line.
Sundberg and colleagues pointed out that, in classical training, sopranos learn to increase the mouth opening as they ascend the scale (Lindblom and Sundberg, 1971, Sundberg and Skoog, 1997) and measured this opening as a function of pitch. They deduced that they were tuning R1 to a value near f0.
Our experiments, using acoustic excitation at the mouth, confirmed this (Joliveau et al., 2004a,b). When f0 was low enough, sopranos used typical values of R1 and R2 for each vowel. However, when f0 was equal or greater to the usual value of R1, they increased R1 so that it was usually slightly higher than f0. For vowels with low R1, this tuning of R1 to f0 starts at lower pitch, and it continues almost up to 1 kHz. Here is a web page about this research, including some sound files.
We don’t know exactly how they learn to do this: it might be that they respond, probably subsciously, when the sound is louder for a given effort. Or it may be that vibrations are easier to produce when the resonance is appropriately tuned. Either way, they could learn to reproduce this effect. A simple model shows that ‘outward opening’ valves (those that open in the direction of the steady flow) tend to be driven most easily at frequencies a little below the resonance: the model valves ‘drive’ inertive loads better than compliant ones (Fletcher, 1993).
What about other singers? In much of the alto range, and for some vowels in the high range of men’s voices, the same problem arises and, although it is much less studied, similar effects are occasionally, but not universally observed (Henrich et al, 2011). Further, some singers seem to tune R1 to the second harmonic (i.e. to 2f0) over a limited range (Smith et al., 2007). In another study, a practitioner of a very loud Bulgarian women’s singing style, was found to tune R1 to 2f0 (Henrich et al., 2007).
Finally, it is worth noting that it is difficult to tune R1 much above 1 kHz, in part because it is hard to open one’s mouth wide enough. Some sopranos who practise the very range of the coloratura soprano, or the whistle voice in pop music, tune R2 to f0, above about C6, which gives them up to another octave or so in their whistle or M3 mechanism (Garnier et al, 2011).
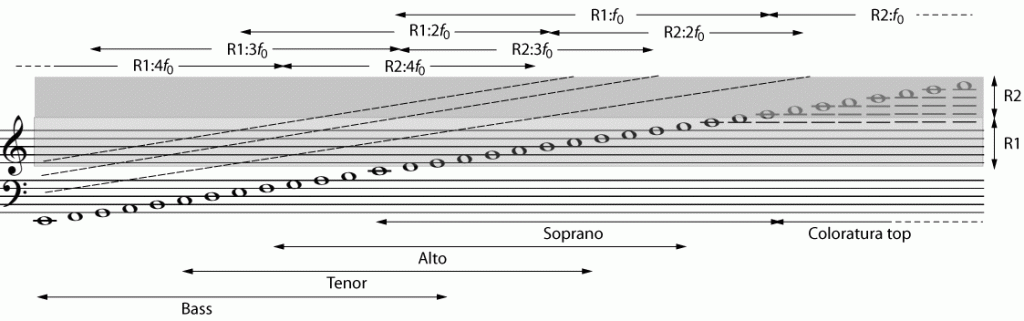
This figure, from Kob et al (2011), shows the different tuning strategies that may be used by different voice categories. Oversimplifying for the sake of brevite, low voices may tune R1 (or R2) to harmonics of the voice. Altos, especially in belting and in the Bulgarian style, tune R1 to the second harmonic. Sopranos tune R1 to f0 up to high C and above that tune R2 to f0. See Henrich et al (2011) for details.
Harmonic singing
In a range of styles known as harmonic or overtone singing, practitioners use a constant, rather low fundamental frequency (in a range where the ear is not very sensitive). They then tune a resonance to select one of the high harmonics, typically from the about the fifth to the twelfth (Kob, 2003; Smith et al., 2007). We have a web site about this.
Is resonance tuning used in speech?
Some speakers (actors, public speakers, teachers) have to speak long and loud. Resonance tuning might be easier for them in one sense: unlike (most) singers, they get to choose the pitch for every word. Some preliminary research suggests that resonance tuning is used in shouting (Garnier et al., submitted).
The singers formant
Male, classically-trained singers often show a spectral peak in the range 2–4 kHz, a range where the ear is quite sensitive. This spectral peak is called the singers formant (Sundberg, 1974, 2001; Bloothooft and Plomp, 1986b). This vocal feature has the further advantage that orchestras have relatively little power in this range, which might allow opera soloists to ‘project’ or to be heard above a large orchestra in a large opera hall.
Singers formants are either weaker, not usually observed, or harder to demonstrate, in women singers (Weiss et al., 2001). This is not surprising: high voices have wide harmonic spacing, which makes it hard to define a formant in the spectrum of any single note. (While one can find a peak in the time-average spectrum of many notes, this is not necessarily the same as a formant, because it depends on which notes are sung.) Further, a resonance in this range is of less use to a high alto or soprano, because the wide harmonic spacing allows a resonance to fall between harmonics. High voices also have the advantage that the fundamental, usually the strongest harmonic, falls in the range of sensitive human hearing. If the gain in a singer’s vocal tract had a bandwidth of a few hundred Hz (the typical width of the singers formant), then for many notes in the high range it would fall between two adjacent harmonics. Finally, high voices can use resonance tuning more effectively than other singers, and may therefore have less need of a singers formant.
Sundberg (1974) attributes the singers formant to a clustering of the third, fourth and/or fifth resonances of the tract. (Measuring the resonances associated with it is an ongoing project in our lab.) Singers produce this formant by lowering the larynx low and narrowing the vocal tract just above the glottis (Sundberg, 1974; Imagawa et al., 1003; Dang and Honda, 1997; Takemoto et al., 2006). A vocal tract with this geometry should work better to transmit power from the glottis to the sound field outside the mouth.
When a strong singers formant is combined with the strong high harmonics produced by rapid closure of the glottis, the effect is a very considerable enhancement of output sound in the range 2-4 kHz – i.e. in a range in which human hearing is very acute and in which orchestras radiate relatively little power. It is not surprising that these are among the techniques used by some types of professional singers who perform without microphones.
Increasing the fraction of power at high frequencies has a further advantage: at wavelengths long in comparison with the size of the mouth, the voice radiates almost isotropically. As the frequency rises and the wavelength decreases, the voice becomes more directional, and proportionally more of the power is radiated in the direction in which the singer faces, which is usually towards the audience (Flanagan 1960; Katz and d’Alessandro, 2007, Kob and Jers, 1999). So increasing the power at high rather than low frequencies via rapid glottal closure and/or a singer’s formant help the singer not to ‘waste’ sound energy radiated up, down, behind and to the sides.
A number of studies have investigated a speaker’s formant or speaker’s ring in the voice of theatre actors or in the speaking voice of singers (Pinczower and Oates, 2005; Bele, 2006; Cleveland et al., 2001; Barrichelo et al., 2001; Nawka et al., 1997). Leino (1993) observed a spectrum enhancement in the voices of actors, but of smaller amplitude than the singing formant, and shifted about 1kHz towards high frequencies. This was interpreted as the clustering of F4 and F5. Bele (2006) reported a lowering of F4 in the speech of professional actors, which contributed to the clustering of F3 and F4 in an important peak. Garnier (2007) also reported such a speaker’s formant in speech produced in noisy environment, with a formant clustering that depended on the vowel.

